Solutions for those exercises.

Exercises

1. Consider the following tree:

   

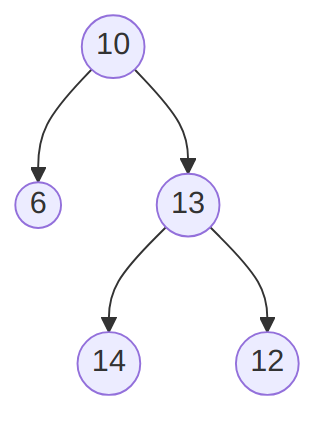
   1. Explain why it is not a binary search tree.

   2. Pick one among inorder, preorder and postorder traversal, and give

      1. A brief description of how it proceeds,

      2. What it would produce for the given tree.

2. Consider the following AVL tree:

   

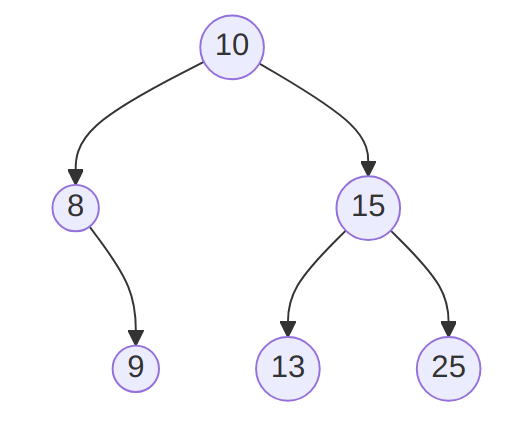
   1. Give its inorder traversal.

   2. Give an order in which the values could have been inserted (for example, even if this is incorrect, “9, 13, 25, …”) to obtain this tree.

   3. Draw next to the drawing the tree obtained after 10 was removed.

3. Consider the following implementation of “random” binary trees:

   public class RBTree<T>
   {
    
   private class Node
       {
       public T Data { get; set; }
       public Node left;
       public Node right;
       public Node(
           T dataP = default(T),
           Node leftP = null,
           Node rightP = null
           )
           {
               Data = dataP;
               left = leftP;
               right = rightP;
           }
       }
    
   private Node root;
    
   public RBTree()
       {
           root = null;
       }
    
   public void Insert(T dataP)
       {
           root = Insert(dataP, root);
       }
    
   private Node Insert(T dataP, Node nodeP)
       {
           if (nodeP == null)
           {
               return new Node(dataP, null, null);
           }
           else
           {
               Random gen = new Random();
               if(gen.NextDouble() > 0.5)
               {
                   nodeP.left = Insert(dataP, nodeP.left);
               }
               else
               {
                   nodeP.right = Insert(dataP, nodeP.right);
               }
           }
           return nodeP;
       }
   }

   Note that the Insert(T dataP, Node nodeP) method uses the gen.NextDouble() > 0.5 test that will be randomly true half of the time, and false the other half.

   1. Explain the T dataP = default(T) part of the Node constructor.

   2. Write a ToString method for the Node class, remembering that only a node Data needs to be part of the string returned.

   3. Write a series of statements that would

      1. create a RBTree object,
      2. insert the values 1, 2, 3, and 4 in it (in this order).

   4. Make a drawing of a possible RBTree obtained by executing your code.

   5. Write a Find method that takes one argument dataP of type T and returns true if dataP is in the RBtree calling object, false otherwise.

4. Given the usual implementation of Node:

   private class Node
   {
       public T Data { get; set; }
       public Node left;
       public Node right;
    
       public Node(T dataP = default(T), Node leftP = null, Node rightP = null)
       {
           Data = dataP;  left = leftP; right = rightP;
       }
   }

   Write an Height property for Node (i.e., a way of computing the longest distance between the calling Node and a leaf).

5. Considering an implementation of binary search trees where T realizes the IComparable<T> interface (i.e., where the .CompareTo method can be used to compare values), write a ValueGreaterThan method that

   • takes an argument dataP of type T,
   • returns
     • true if there is a value greater than or equal to dataP in the binary search tree,
     • false if there is no value greater than dataP in the binary search tree, or if the tree is empty.