Introduction

Abstract Data Type

Described abstractly, a priority queue is (the differences with queue are in bold):

a finite collection of elements, endowed with a priority
in no particular order,
that may contain the same element multiple times.

Generally, it has operations to…

… create an empty priority queue,
… test for emptiness,
… add an element with a given priority,
… remove the element with the highest priority,
… increase the priority of a particular element.

Letting a greater priority means “more important” is called a max-priority queue, it is also possible to implement min-priority queue, where the most element important are the ones with the lowest priority. In both cases, a decision must be made if multiple elements have the same priority: we can decide arbitrarily, using the element value, take the “first one” in the structure, etc.

Exactly like a people waiting at the ER, priority queues implement a “most-important-in-first-out” principle. Our examples will use the Emergency Severity Index, which ranges from 1 (most urgent) to 5 (less urgent).

Possible Implementation

Using Arrays

Here is an implementation of priority queues using arrays:

using System; // This is required for the exception.
 
class PQueue<TPriority, TValue>
  where TPriority : IComparable<TPriority>
{
  class Cell
  {
    public TPriority Priority { get; set; }
    public TValue Value { get; set; }
 
    public Cell(TPriority priorityP, TValue valueP)
    {
      Priority = priorityP;
      Value = valueP;
    }
 
    public override string ToString()
    {
      return Value + " (priority: " + Priority + ")";
    }
  }
 
  private Cell[] mArray;
 
  public PQueue(int sizeP = 10)
  {
    mArray = new Cell[sizeP];
  }
 
  public void Add(TPriority priorityP, TValue valueP)
  {
    // slot is the index where we will add the element
    int slot = -1;
    // index is where we are currently looking for
    // a slot in the arry.
    int index = 0;
    while (index < mArray.Length && slot == -1)
    {
      if (mArray[index] == null)
      {
        slot = index;
      }
      else
      {
        index++;
      }
    }
    if (slot == -1)
    {
      throw new ApplicationException(
        "Queue is full, cannot add "
          + valueP
          + " with priority "
          + priorityP
          + "."
      );
    }
    else
    {
      mArray[slot] = new Cell(priorityP, valueP);
    }
  }
 
  public int MinPriority()
  {
    int index = 0;
    // We begin by looking for a value
    // in mArray that is not null.
    bool notNull = false;
    while (index < mArray.Length && !notNull)
    {
      if (mArray[index] != null)
      {
        // We found a value that is not null.
        notNull = true;
      }
      else
      {
        index++;
      }
    }
    // If we exit and notNull is still false,
    // it means there is no non-null cell in
    // the array.
    if (!notNull)
    {
      throw new ApplicationException(
        "Queue is empty, no index with minimal priority."
      );
    }
    // Minimal priority found "so far".
    TPriority minP = mArray[index].Priority;
    // Index of the minimal priority found "so far".
    int minI = index;
    while (index < mArray.Length)
    {
      // The following if is crucial: there may
      // be null values in the array, and we should
      // not try to access the Priority property
      // if mArray[index] is null.
      if (mArray[index] != null)
      {
        // If we found a lower priority,
        // we update the minP and minI
        // values.
        if (mArray[index].Priority.CompareTo(minP) < 0)
        {
          minP = mArray[index].Priority;
          minI = index;
        }
      }
      index++;
    }
    return minI;
  }
 
  public TValue Peek()
  {
    // Looking at the most urgent Cell
    // uses MinPriority.
    return mArray[MinPriority()].Value;
  }
 
  public string Extract()
  {
    // Removing the most urgent Cell
    // relies also on MinPriority().
    int minE = MinPriority();
    Cell cellE = mArray[minE];
    mArray[minE] = null;
    return cellE.ToString();
  }
 
  public override string ToString()
  {
    string ret = "";
    for (int i = 0; i < mArray.Length; i++)
    {
      if (mArray[i] != null)
      {
        ret += mArray[i].ToString();
      }
      else
      {
        ret += "(empty)";
      }
      ret += "\n";
    }
    return ret;
  }
}

(Download this code)

This implementation as the following performance:

Add is $O (n)$ , it may take $n$ steps to find an empty slot,
MinPriority is also $O (n)$ , we will have to go through the entire array to find the Cell with the highest priority.
Peek and Extract both rely on MinPriority, so they are also $O (n)$ .

Using Lists

An implementation using lists would be very similar to the one using array, except that Add would be $O (c)$ , since inserting in a list can simply be done at the beginning.

Using Heaps

A maximally efficient implementation of priority queues is given by heaps, which is

A complete binary tree¹ (that we will represent in an array),
Such that the priority of every (non-root) node is greater than the priority of its parent (remember that we are implementing a min-priority queue, so a lowest priority means “comes first”).

Note that this is different from being a binary search tree. We begin by explaining informally the main principles, before commenting on the implementation.

Representing complete binary trees using arrays

A binary heap is often implemented as an array. Consider the following binary tree (we will take the priority of the node to be its value in the following):

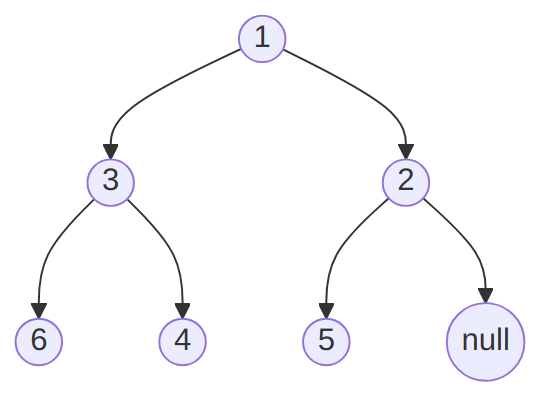
Heap example, represented as a complete binary tree (text version, image version, svg version)

It is a heap, but not a binary search tree. It can be represented as the following array:

Index	0	1	2	3	4	5	6	7
Node	`null`	1	3	2	6	4	5	`null`

It can help to see the tree as follows²:

1
└── 3
│   └──── 6
│   └────────4 
└──────2
       └──────── 5
       └────────────(null)

so that reading it right to left gives the array pictured above.

The reason why we start at index 1 and not 0 is because it makes the following calculation easier³. Indeed, each element at index $i$ has

its children at indices $2 \times i$ and $(2 \times i) + 1$ ,
its parent at index $⌊ i /2 ⌋$ for $⌊ \cdot ⌋$ the floor function (i.e., $⌊ 1.5 ⌋ = 1$ ).

Inserting into a heap

To insert an element to a heap, we perform the following steps:

Add the element to the bottom level of the heap at the leftmost open space (or “start” a new level if the last level is full).
Compare the added element with its parent; if they are in the correct order, stop.
If not, swap the element with its parent and return to the previous step.

Imagine we want to insert $- 1$ in our previous example, we would:

Add $- 1$ as the right child of $2$ ,
Swap $- 1$ and $2$ ,
Swap $- 1$ and $1$ ,
Be done.

In terms of array representation, we would obtain (with the values that changed in bold):

Index	0	1	2	3	4	5	6	7
Node	`null`	-1	3	1	6	4	5	2

Deleting from a heap

Extracting the element with the lowest priority is easy: it is located at the root of the tree, or at index 1 in the array representation. The challenge is to restore “the heap property”, which is done as follows:

Replace the root of the heap with the last element on the last level.
Compare the new root with its children; if they are in the correct order, stop.
If not, swap the element with one of its children and return to the previous step (swaping with the smaller child in a min-heap).

The 2nd and 3rd steps are called “percolate-down”: the idea is that the element that is at the root will “go down” the heap by swapping with elements with smaller priority. At each step, we compare its priority with its children priority, and swap it with the children with the lowest priority if it is lower than its own. When both children have a higher than or equal priority to its own, we know we are done and can stop.

Implementing priority queue using heaps implemented as arrays

using System;
using System.Collections.Generic;
 
public class PQueue<TPriority, TValue>
  where TPriority : IComparable<TPriority>
{
    class Cell
    {
        public TPriority Priority { get; set; }
        public TValue Value { get; set; }
 
        public Cell(TPriority priorityP, TValue valueP)
        {
            Priority = priorityP;
            Value = valueP;
        }
 
        public override string ToString()
        {
            return Value + " (priority: " + Priority + ")";
        }
    }
 
    private Cell[] mArray;
 
    // Number of items in queue.
    private int count = 0;
 
    public PQueue(int size = 100)
    {
        if (size < 10)
            size = 10;
        mArray = new Cell[size];
    }
 
    public bool IsEmpty()
    {
        return count == 0;
    }
 
    public bool IsFull()
    {
        return (count == mArray.Length - 1);
    }
 
    public void Clear()
    {
        count = 0;
    }
 
    public TValue Peek()
    {
        if (IsEmpty())
            throw new ApplicationException(
              "Queue is empty, no most urgent value."
            );
        return mArray[1].Value;
    }
 
    public void Add(TPriority priorityP, TValue valueP)
    {
        if (IsFull())
            throw new ApplicationException(
              "Queue is full, cannot add "
                + valueP
                + " with priority "
                + priorityP
                + "."
            );
 
        // Otherwise, we will be able to add an element,
        // so count must increment.
        count++;
        // We now look for a place to insert the value,
        // we call it (empty) "slot".
        int slot = count;
        // As long as slot > 1 and priorityP is less than
        // the priority at slot / 2…
        while (
          slot > 1
          && priorityP.CompareTo(mArray[slot / 2].Priority) < 0
        )
        {
            mArray[slot] = mArray[slot / 2];
            slot /= 2;
            // We divide slot by 2
            // and move the data at slot / 2 at slot.
        }
        // Once this is done, we can insert the 
        // new value in the slot.
        mArray[slot] = new Cell(priorityP, valueP);
    }
 
    public TValue Extract()
    {
        if (IsEmpty())
            throw new ApplicationException(
              "Queue is empty, cannot extract from it."
            );
 
        // Save the data to be returned.
        TValue cellValue = mArray[1].Value;
 
        // Replace the root with the last element
        // on the last level.
        mArray[1] = mArray[count];
        // We have one less element now.
        count--;
 
        // Move the lowest child up until we've found the right spot
        // for the cell moved from the last level to the root.
        PercolateDown(1);
        return cellValue;
    }
 
    private void PercolateDown(int indexP)
    {
        // "PercolateDown", starting at
        // indexP.
        int child;
        // Save the slot's cell.
        Cell travellingCell = mArray[indexP];
 
        bool found = false;
        // Keep going down the tree until the last level
        // or until we found the place where it belongs.
        while (indexP * 2 <= count && !found)
        {
            // Get the right child.
            child = indexP * 2;
            // Now, we check right and left child 
            // and put lowest one in the child variable
            if (child != count)
            { // If there is a left child…
                if (mArray[child + 1]
                        .Priority.CompareTo(mArray[child].Priority) < 0)
                {
                    // … and it has a lowest priority, use it.
                    child++;
                }
            }
 
            // At this point, we know that child
            // refers the child with the lowest
            // priority.
 
            // Now, we put the lowest child in slot
            // if its priority
            // is less than the priority of the cell
            // currently in the slot.
            if (
              mArray[child].Priority.CompareTo(travellingCell.Priority)
              < 0
            )
            {
                mArray[indexP] = mArray[child];
            }
            else
            {
                // Otherwise we are done.
                found = true;
            }
            // If we are not done,
            // we update the value for indexP.
            if (!found)
            {
                indexP = child;
            }
        }
        // found right spot of slot's original value, put it back into tree
        mArray[indexP] = travellingCell;
    }
 
    public override string ToString()
    {
        string returned = "";
        for (int i = 1; i <= count; i++)
        {
            returned += mArray[i].ToString() + "; ";
        }
        return returned;
    }
}

(Download this code)

A complete binary tree is such that all levels are filled completely except the lowest level, which is filled from as left as possible. ↩
Symbols courtesy of https://gist.github.com/GeorgeHernandez/10dcbb5fd6ca8b087d169d5a44d72cd2. ↩
The difference can be looked up on wikipedia, it is mostly a matter of substracting or adding 1 at various places. ↩

ℙrinℂomℙ

Explorer

Priority Queues

Introduction

Abstract Data Type

Possible Implementation

Using Arrays

Using Lists

Using Heaps

Representing complete binary trees using arrays

Inserting into a heap

Deleting from a heap

Implementing priority queue using heaps implemented as arrays

Graph View

Table of Contents

Backlinks

ℙrinℂomℙ

Explorer

Priority Queues

Introduction

Abstract Data Type

Possible Implementation

Using Arrays

Using Lists

Using Heaps

Representing complete binary trees using arrays

Inserting into a heap

Deleting from a heap

Implementing priority queue using heaps implemented as arrays

Footnotes

Graph View

Table of Contents

Backlinks