Introduction

A binary tree is a precise mathematical concept that can be defined as a restriction on graphs. As an abstract data type, it generally uses the following definitions:

• A binary tree is made of nodes, each of which holds one value, can have up to 2 children.
• A (rooted) binary tree has exactly one node with 0 parent (that is not the child of any other node), called the root. Except for the root, all the nodes have exactly one parent.
• A node without children is called a leaf.
• The depth of a node is the distance (i.e., the number of times we must go to its parent) from it to the root. This means in particular that the depth of the root is $0$.
• The depth of a tree is the maximum depth of the nodes it contain.
• A subtree is the tree obtain by considering a particular node in a tree as the root of the tree made of all the nodes “below” it, starting with its children.

From there, operations generally include, as usual

• Creating an empty tree,
• Adding a node to a tree,
• Finding the smallest value in the tree,
• Removing a node holding a specific value from the tree,
• etc.

In the following example:

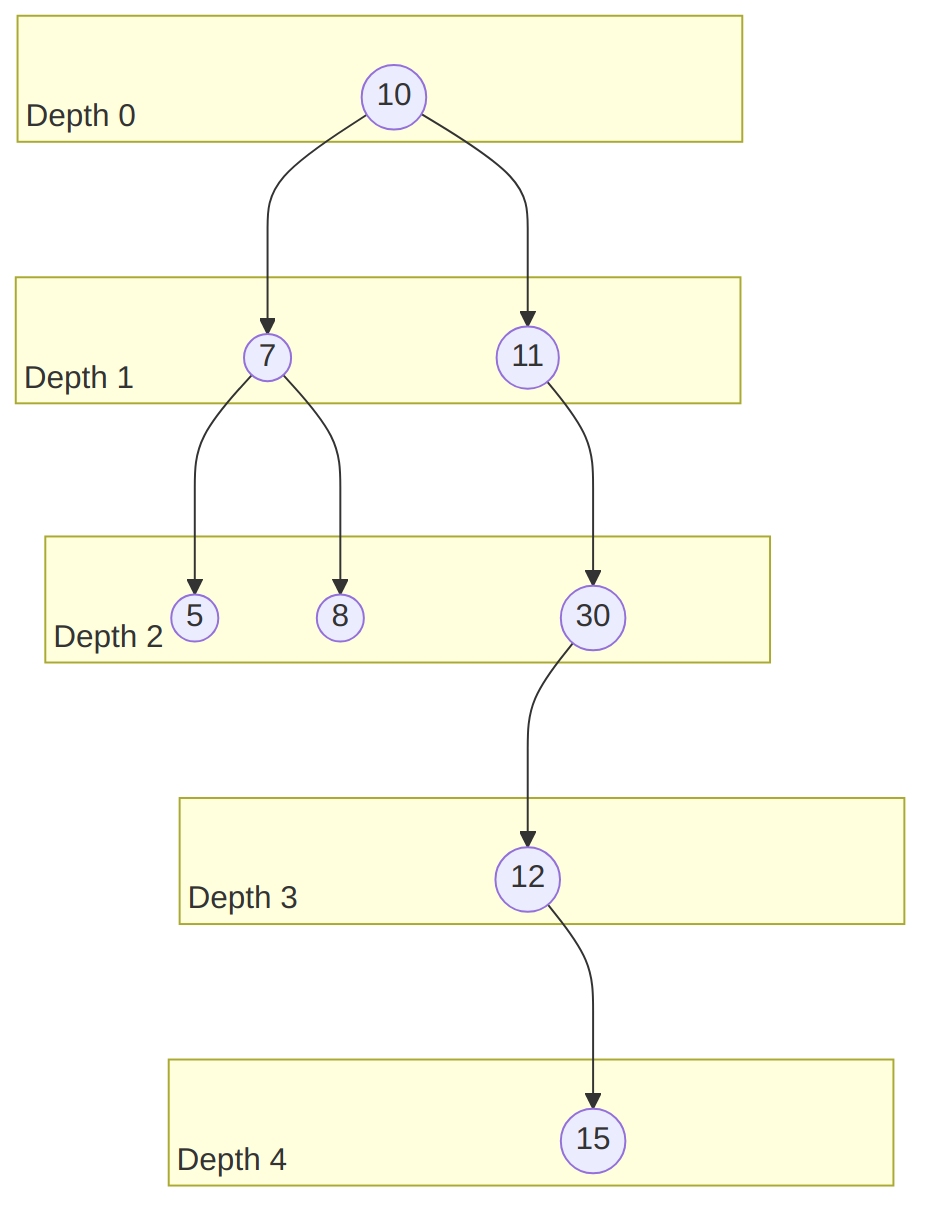
• The root holds the value 10,
• The root has two children, holding the values 7 and 11,
• The node holding the value 5 has $0$ children, hence it is a leaf,
• The node with value 11 has one child (holding the value 30): we call it “the right child”, and observe that the node holding the value 11 has no “left child”,
• The depth of the tree is $4$,
• The nodes holding the values 7, 5 and 8 taken together form a subtree, of depth $1$.

Possible Implementation

Binary Tree

We implemented the binary tree class abstractly, because two methods will be missing at the beginning: how to insert a value, and how to delete a value (we will add them later on, in a class that will inherit from this BTree class). This is the reason why we mark the Node class as protected below, and not private: it will still be accessible by the class inheriting from BTree.

Node Class

Defining a BTree class start by defining a Node class:

  protected class Node
  {
    public T Data { get; set; }
    public Node left;
    public Node right;
 
    public Node(
      T dataP = default(T),
      Node leftP = null,
      Node rightP = null
    )
    {
      Data = dataP;
      left = leftP;
      right = rightP;
    }
        // Displaying a Node is only 
        // displaying its data.
    public override string ToString()
    {
      return Data.ToString();
    }
  }

(Download this code)

As we can see, a Node has three elements:

• Data is the value it is holding,
• left denotes its “left child” (which is a Node, possibly null),
• right denotes its “right child” (which is a Node, possibly null),

If we wanted to be more technically correct in our drawing, we would explicitly label some nodes as null, and the previous tree would actually be as follows:

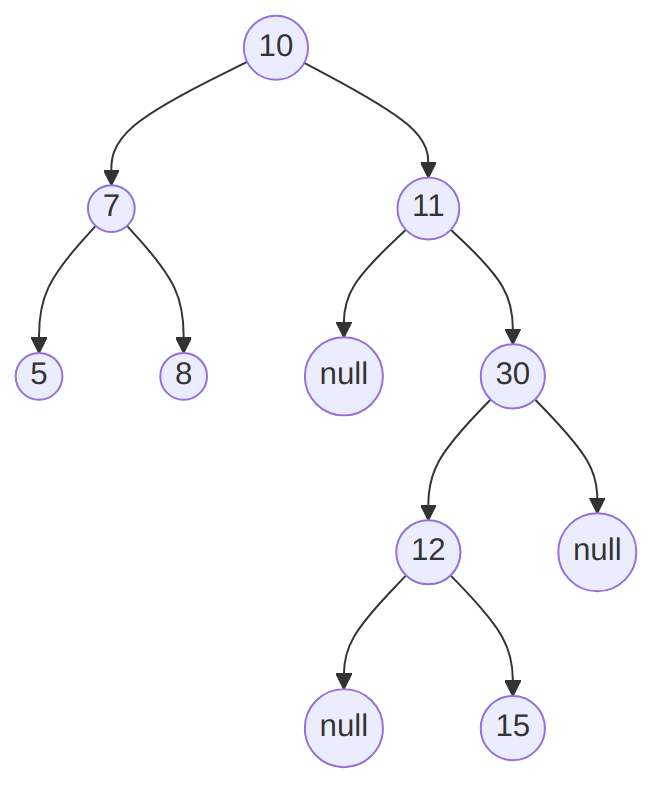
Initializing

A BTree object is simply the root Node, and we can construct, empty, and test for emptiness accordingly:

  protected Node root;
 
  public BTree()
  {
    root = null;
  }
 
  public void Clear()
  {
    root = null;
  }
 
  public bool IsEmpty()
  {
    return root == null;
  }

(Download this code)

Computing the Depth of the tree

Now, assume that we are given a BTree object. How can we compute its depth? Its depth is the maximum depth of the nodes it contain. However, only the root knows its depth (it is $0$), all the other nodes do not know their depth, only that they have 0, 1 or 2 children.

Of course, if the BTree is null or if its root has $0$ children, then deciding its depth is easy: it is $0$. Otherwise, the idea is that each tree knows that its depth is $1$ more than the depth of the its two sub-trees: remains to find which sub-tree has the biggest depth. For this, we will use recursion.

In short, for a tree to determine its node, it needs to

• Have its root “ask its children” what their deepest node is,
• Take the maximum value returned.

For the root’s children to determine what the deepest node under them is, they need both to

• “Ask their children” what is their deepest node,
• Take the maximum value returned.

Etc., etc. Hence, we get:

 
  public int Depth()
  {
    int depth = 0;
    if (root != null)
    {
      depth = Depth(root, 0);
    }
    return depth;
  }
 
  private int Depth(Node nodeP, int depth)
  {
    // "Unless proven otherwise",
    // we assume that the depth of the
    // node is the depth it received
    // as argument.
    int result = depth;
    // We assume the depth of
    // its right sub-tree
    // is 0.
    int depthL = 0;
    if (nodeP.left != null)
    {
      // If its left sub-tree is not null,
      // we inquire about its depth,
      // knowing that it will be 1 more
      // than the depth of the current node.
      depthL = Depth(nodeP.left, result + 1);
    }
    // We proceed similarly for the
    // left sub-tree.
    int depthR = 0;
    if (nodeP.right != null)
    {
      depthR = Depth(nodeP.right, result + 1);
    }
    // Finally, if at least one sub-tree
    // is not null, we take the max of their
    // depths to be the depth of the tree
    // starting with our current node.
    if (nodeP.left != null || nodeP.right != null)
    {
      result = Math.Max(depthL, depthR);
    }
    return result;
  }

(Download this code)

Note that we have two recursive calls: one for the left Node, one for the right Node (if they are not null).

Displaying Trees

There are essentially three ways of “linearizing” a tree (that is, listing its value in a sequence), depending how we organize the recursive calls.

• Inorder traversal displays

  • First the left sub-tree,
  • Secondly the data held by the current node,
  • Thirdly the right sub-tree.

  For our recurring example, we obtain “5 7 8 10 11 12 15 30”.

• Preorder traversal displays

  • First the data held by the current node,
  • Secondly the left sub-tree,
  • Thirdly the right sub-tree.

  For our recurring example, we obtain “10 7 5 8 11 30 12 15”.

• Postorder traversal displays

  • First the left sub-tree,
  • Secondly the right sub-tree,
  • Thirdly the data held by the current node.

  For our recurring example, we obtain “5 8 7 15 12 30 11 10”.

The code for all three methods will be extremely similar, the only difference is the order in wich we make the recursive calls and add the data held by the current node to the string returned:

  // Inorder traversal
  // "Left, data, right"
  public string TrasverseI()
  {
    string returned = "";
    if (root != null)
    {
      returned += TraverseI(root);
    }
    return returned;
  }
 
  private string TraverseI(Node nodeP)
  {
    string returned = "";
    if (nodeP != null)
    {
      returned += TraverseI(nodeP.left);
      returned += nodeP.Data + " ";
      returned += TraverseI(nodeP.right);
    }
    return returned;
  }
 
  // Preorder traversal
  // "Data, left, right"
  public string TrasversePr()
  {
    string returned = "";
    if (root != null)
    {
      returned += TraversePr(root);
    }
    return returned;
  }
 
  private string TraversePr(Node nodeP)
  {
    string returned = "";
    if (nodeP != null)
    {
      returned += nodeP.Data + " ";
      returned += TraversePr(nodeP.left);
      returned += TraversePr(nodeP.right);
    }
    return returned;
  }
 
  // Postorder traversal
  // "Left, right, data"
  public string TrasversePo()
  {
    string returned = "";
    if (root != null)
    {
      returned += TraversePo(root);
    }
    return returned;
  }
 
  private string TraversePo(Node nodeP)
  {
    string returned = "";
    if (nodeP != null)
    {
      returned += TraversePo(nodeP.left);
      returned += TraversePo(nodeP.right);
      returned += nodeP.Data + " ";
    }
    return returned;
  }

(Download this code)

Finding a Value

Finding a value is also a recursive process: a BTree will contain a value dataP if…

• its root hold dataP,
• its right- or left-subtree contain dataP.

The subtrees will determine if they hold dataP by determining if

• their roots hold dataP,
• their right- or left-subtrees contain dataP.

As we can see, we once again need to have a method with two recursive calls:

 
  public virtual bool Find(T dataP)
  {
    bool found = false;
    if (root != null)
    {
      found = Find(root, dataP);
    }
    return found;
  }
 
  private bool Find(Node nodeP, T dataP)
  {
    bool found = false;
    if (nodeP != null)
    {
      if (nodeP.Data.Equals(dataP))
      {
        found = true;
      }
      else
      {
        found =
          Find(nodeP.left, dataP)
          || Find(nodeP.right, dataP);
      }
    }
    return found;
  }

(Download this code)

Finally, observe that we mark the Find method as virtual because we will override it for something more efficient once we look at binary search trees.

Binary Search Tree

A binary search tree (BST) is a specific type of binary tree that ensures that

• each node’s value is greater than all the values stored in its left subtree,
• each node’s value is less than all the values stored in its right subtree,
• a value cannot occur twice.

Our recurring example happens to be a binary search tree:

• All the values “to the left of” the root are less than $10$,
• All the values “to the right of” the root are greater than $10$,
• All the values “to the left of” the left child of the root are less than $8$,
• All the values “to the right of” the left child of the root are greater than $8$,
• etc.

Note that this is the reason why the node with value $30$ is drawn “to the right of” the node with value $11$: we always need to make the difference between left and right children, even if there is only one child. A tree almost identical to our recurring example, but where $30$ was at the right of the node holding the value $11$ would not be a binary search tree, but simply a binary tree.

Implementation detail

Note that since we need to be able to compare our values, we must tell C# that we will not just be using any generic type T, but a type that realizes the IComparable interface. This forces T to have a CompareTo method, that we will use to compare the data held by the nodes as follows:

dataP.CompareTo(nodeP.Data)

will return

• a value less than $0$ if dataP < nodeP.Data,
• a value greater than $0$ if dataP > nodeP.Data.

Similarly to the Equals method, this is because the > and < operators are not overloaded by default, so we must use this more convoluted way of determining if dataP is less than or greater than nodeP.Data. Of course, if neither is true, it means that dataP is equal to nodeP.Data.

Insertion

To insert in a binary search tree, we must respect the binary search tree definition, meaning that we must:

• refuse to insert a value that is already present,
• insert a value “in its right place”, i.e., to the right of nodes containing smaller values, and to the left of nodes containing greater values.

  public override void Insert(T dataP)
  {
    root = Insert(dataP, root);
  }
 
  private Node Insert(T dataP, Node nodeP)
  {
    if (nodeP == null)
    {
      return new Node(dataP, null, null);
    }
    else if (dataP.CompareTo(nodeP.Data) < 0) // dataP < nodeP.Data
    {
      nodeP.left = Insert(dataP, nodeP.left);
    }
    else if (dataP.CompareTo(nodeP.Data) > 0) // dataP > nodeP.Data
    {
      nodeP.right = Insert(dataP, nodeP.right);
    }
    else
    {
      throw new ApplicationException(
        "Value " + dataP + " already in tree."
      );
    }
    return nodeP;
  }

(Download this code)

Note that it implies that creating a BSTree by inserting, for example

• 10, 6, 13, 12 and 14
• 14, 12, 13, 6 and 10

will result in different trees.

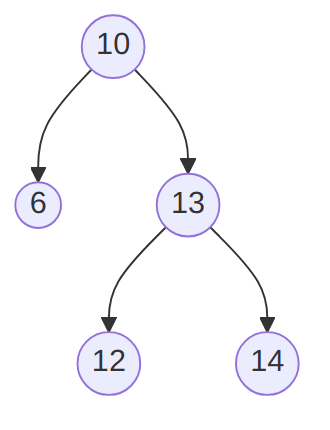
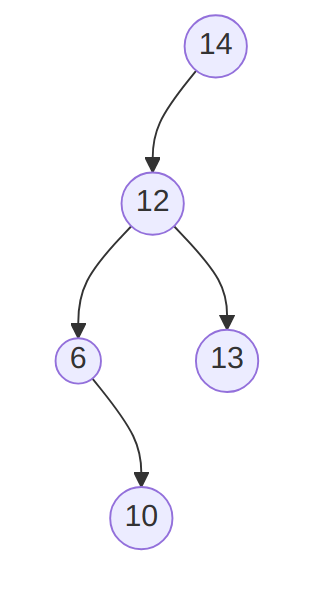
To begin with, the first will have 10 on its root while the other will have 14!

Finding

To find a value in a binary search tree, we can leverage its principles to make only one recursive call instead of two (as in our previous Find method for BTree). Indeed, if the value we are looking for is …

• the same as the value held by the current node, we are done,
• less than the value held by the current node, we only need to explore the left sub-tree,
• greater than the value held by the current node, we only need to explore the right sub-tree.

Similarly, finding the smallest value is easy: it will be the one held by the left-most node!

 
    public override bool Find(T dataP)
    {
        bool found = false;
        if (root != null)
        {
            found = Find(root, dataP);
        }
        return found;
    }
 
    private bool Find(Node nodeP, T dataP)
  {
    bool found = false;
    if (nodeP != null)
    {
      if (nodeP.Data.Equals(dataP))
      {
        found = true;
      }
      else
      {
        if (dataP.CompareTo(nodeP.Data) < 0) // dataP < nodeP.Data
        {
          found = Find(nodeP.left, dataP);
        }
        else if (dataP.CompareTo(nodeP.Data) > 0) // dataP > nodeP.Data
        {
          found = Find(nodeP.right, dataP);
        }
      }
    }
    return found;
  }
 
  public T FindMin()
  {
    if (root == null)
    {
      throw new ApplicationException(
        "Cannot find a value in an empty tree!"
      );
    }
    else
    {
      return FindMin(root);
    }
  }
 
  private T FindMin(Node nodeP)
  {
    T minValue;
    if (nodeP.left == null)
    {
      minValue = nodeP.Data;
    }
    else
    {
      minValue = FindMin(nodeP.left);
    }
    return minValue;
  }

(Download this code)

Deleting

Deleting is a more convoluted operation:

 
  public override bool Delete(T dataP)
  {
    return Delete(dataP, ref root);
  }
 
  private bool Delete(T dataP, ref Node nodeP)
  {
    bool found = false;
    if (nodeP != null)
    {
      if (dataP.CompareTo(nodeP.Data) < 0) // dataP < nodeP.Data
      {
        found = Delete(dataP, ref nodeP.left);
      }
      else if (dataP.CompareTo(nodeP.Data) > 0) // dataP > nodeP.Data
      {
        found = Delete(dataP, ref nodeP.right);
      }
      else // We found the value!
      {
        found = true;
        if (nodeP.left != null && nodeP.right != null)
        {
          nodeP.Data = FindMin(nodeP.right);
          Delete(nodeP.Data, ref nodeP.right);
          // Or we could replace with the largest
          // value in the left subtree.
        }
        else
        {
          if (nodeP.left != null)
          {
            nodeP = nodeP.left;
          }
          else
          {
            nodeP = nodeP.right;
          }
        }
      }
    }
    return found;
  }

(Download this code)