Exercises

Consider the following tree:
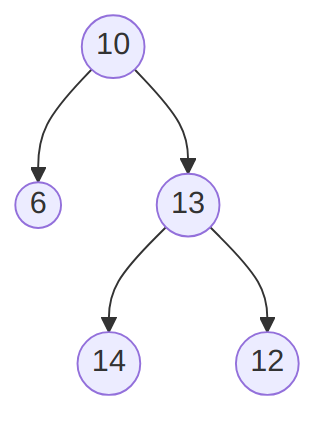
1. Explain why it is not a binary search tree.
  
  Solution
  
  The left child of the node with value 13 has value 14, which is greater than 13, hence violating the binary search tree principle that values in the left sub-tree should be strictly less than the value in the root of the subtree. The same goes for 12.
2. Pick one among inorder, preorder and postorder traversal, and give
  1. A brief description of how it proceeds,
    Solution
    
    One among the following:
    - Inorder traversal processes (recursively) first the left subtree, then the data at the root, then the right subtree.
    - Preorder traversal processes (recursively) first the data at the root, then the left subtree, then the right subtree.
    - Postorder traversal processes (recursively) first the left subtree, then the right subtree, then the data at the root.
  2. What it would produce for the given tree.
    Solution
    
    One among the following:
    - Inorder gives 6, 10, 14, 13, 12
    - Preorder gives 10, 6, 13, 14, 12
    - Postorder gives 6, 14, 12, 13, 10
Consider the following AVL tree:
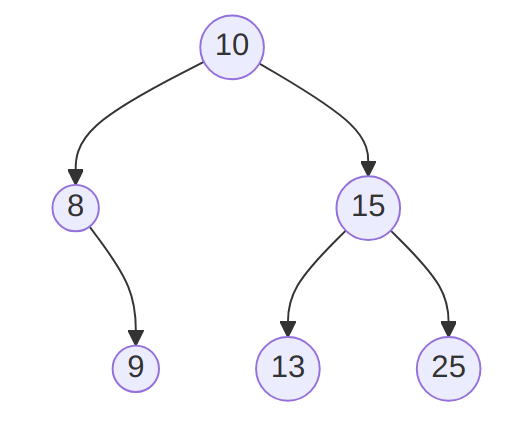
1. Give its inorder traversal.
  
  Solution
  
  8, 9, 10, 13, 15, 25
2. Give an order in which the values could have been inserted (for example, even if this is incorrect, “9, 13, 25, …”) to obtain this tree.
  Solution
  
  The values could have been inserted as
  - 10, 8, 15, 9, 13, 25
  - 10, 15, 8, 9, 13, 25 (permuting 15 and 8),
  - 10, 8, 15, 13, 25, 9 (permuting 13, 25, and 9),
  or some other variations: the important aspects are:
  1. Start with 10,
  2. Do not, while inserting the tree, make it un-balanced (otherwise, the tree would re-balance itself and 10 would not be the root).
  If one wants to leverage re-balancing of the tree, then we can use the following sequence:
  - 15, 13, 25, 10, 8, 9
  Indeed, the tree remains balanced until 9 is inserted: inserting 9 triggers a re-balancing that actually produce the tree given as an example. An example of an incorrect sequence could be
  - 15, 13, 8, 9, 25, 10,
  as this produces a tree with 13 at its root.
3. Draw next to the drawing the tree obtained after 10 was removed.
  Solution
  
  There are two strategies after the root was removed:
  - Replacing it with the greatest value on the sub-tree to the left,
  - Replacing it with the lowest value on the sub-tree to the right.
  The second strategy, which is the one implemented in the lecture notes, gives:

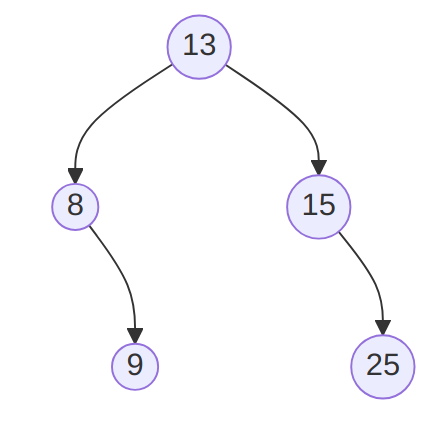
Consider the following implementation of “random” binary trees:

public class RBTree<T>
{
 
private class Node
    {
    public T Data { get; set; }
    public Node left;
    public Node right;
    public Node(
        T dataP = default(T),
        Node leftP = null,
        Node rightP = null
        )
        {
            Data = dataP;
            left = leftP;
            right = rightP;
        }
    }
 
private Node root;
 
public RBTree()
    {
        root = null;
    }
 
public void Insert(T dataP)
    {
        root = Insert(dataP, root);
    }
 
private Node Insert(T dataP, Node nodeP)
    {
        if (nodeP == null)
        {
            return new Node(dataP, null, null);
        }
        else
        {
            Random gen = new Random();
            if(gen.NextDouble() > 0.5)
            {
                nodeP.left = Insert(dataP, nodeP.left);
            }
            else
            {
                nodeP.right = Insert(dataP, nodeP.right);
            }
        }
        return nodeP;
    }
}

Note that the Insert(T dataP, Node nodeP) method uses the gen.NextDouble() > 0.5 test that will be randomly true half of the time, and false the other half.

Explain the T dataP = default(T) part of the Node constructor.

Solution

This makes the first argument of the constructor optional: if no value is provided, then the default value for T is used. For example, for int, then 0 would be used.
Write a ToString method for the Node class, remembering that only a node Data needs to be part of the string returned.
Solution
```
 public override string ToString()
 {
     return Data.ToString();
 }
```

Write a series of statements that would

create a RBTree object,

insert the values 1, 2, 3, and 4 in it (in this order).

Solution

 RBTree<int> btree = new RBTree<int>();
 btree.Insert(1);
 btree.Insert(2);
 btree.Insert(3);
 btree.Insert(4);

Make a drawing of a possible RBTree obtained by executing your code.

Solution

Any binary tree containing 1, 2, 3 and 4, with 1 at the root, 2 a child of 1, 3 a child of 1 or 2, and 4 a child of 1, 2 or 3, is correct. One such example is:

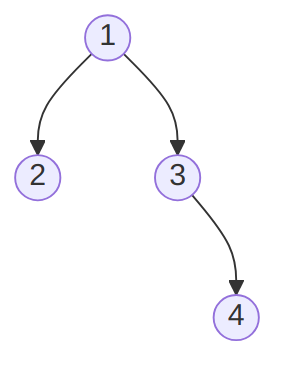
Write a Find method that takes one argument dataP of type T and returns true if dataP is in the RBtree calling object, false otherwise.

Solution

 public bool Find(T dataP)
 {
     bool found = false;
     if (root != null)
     {
         found = Find(root, dataP);
     }
     return found;
 }
 
 private bool Find(Node nodeP, T dataP)
 {
     bool found = false;
     if (nodeP != null)
     {
         if (nodeP.Data.Equals(dataP))
         {
             found = true;
         }
         else
         {
             found =
             Find(nodeP.left, dataP)
             || Find(nodeP.right, dataP);
         }
     }
     return found;
 }

Given the usual implementation of Node:

private class Node
{
    public T Data { get; set; }
    public Node left;
    public Node right;
 
    public Node(T dataP = default(T), Node leftP = null, Node rightP = null)
    {
        Data = dataP;  left = leftP; right = rightP;
    }
}

Write an Height property for Node (i.e., a way of computing the longest distance between the calling Node and a leaf).

Solution

The one provided in the lecture notes is:

    public int Height
    {
      get
      {
        int height = 0;
        if (left != null && right != null)
        {
          height = Math.Max(left.Height, right.Height) + 1;
        }
        else if (left != null)
        {
          height = left.Height + 1;
        }
        else if (right != null)
        {
          height = right.Height + 1;
        }
        // The last case is if both children
        // are null, in which case the height
        // remains 0.
        return height;
      }
    }

(Download this code)

Considering an implementation of binary search trees where T realizes the IComparable<T> interface (i.e., where the .CompareTo method can be used to compare values), write a ValueGreaterThan method that

takes an argument dataP of type T,
returns
- true if there is a value greater than or equal to dataP in the binary search tree,
- false if there is no value greater than dataP in the binary search tree, or if the tree is empty.

Solution

The one provided in the lecture notes is:

 
  public bool ValueGreaterThan(T dataP)
  {
    bool returned = false;
    if (root != null)
    {
      returned = ValueGreaterThan(dataP, root);
    }
    return returned;
  }
 
  private bool ValueGreaterThan(T dataP, Node nodeP)
  {
    bool returned = false;
    if (nodeP != null)
    {
      if (dataP.CompareTo(nodeP.Data) > 0) // dataP > nodeP.Data
        return ValueGreaterThan(dataP, nodeP.right);
      // We only need to go right, since values will decrease
      // if we go left.
      else
        returned = true;
    }
    return returned;
  }

(Download this code)

ℙrinℂomℙ

Explorer

Trees (Solutions)

Exercises

Graph View

Backlinks