Introduction
An AVL tree (for Adelson-Velsky and Landis, their two inventors) is a particular type of binary search tree, with the self-balancing property. In a nutshell, self-balancing trees always thrive to keep their height as small as possible when inserting and deleting values.
Indeed, consider a binary search tree using the Insert method defined
previously to insert the values 1, 2, 3, …, 100 (in that order). Then
we obtain a tree that is a line, with each node having at most 1 child.
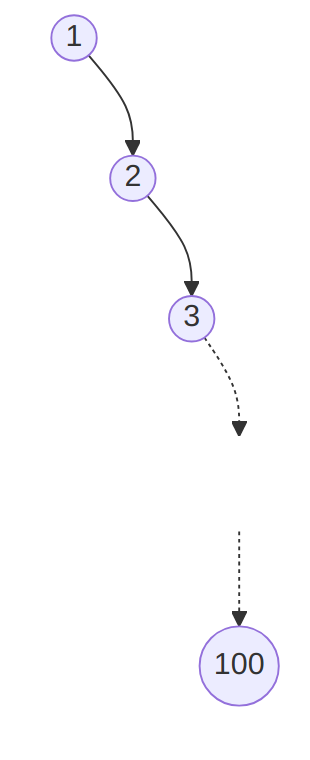
The resulting tree has for height the number of nodes, 100 in this case. Since looking up a value or inserting a value is linear in the height of the tree, this means that those operations takes 100 operations: the benefits of using a tree instead of a list is lost!
The resulting tree would be much more efficient if we were leveraging the property of binary search tree to “balance” the values and obtain something … more balanced, with a “maximal number of children” for each nodes.
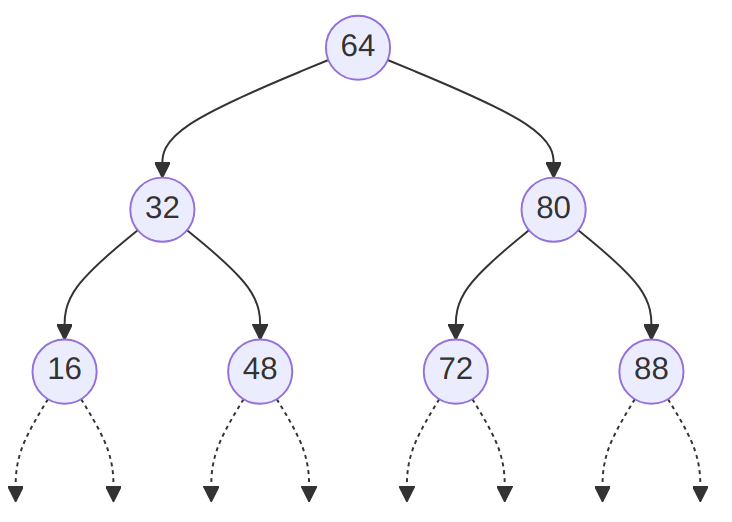
This is precisely the point of AVL trees, which are binary search trees with the additional property:
The heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, re-balancing is done to restore this property.
where
- the height of a node is the number of edges on the longest path from the node to a leaf.
- the depth of a node is the number of edges from the node to the tree’s root node.
A good way of remembering the difference is to observe that we measure the height of a person from toe (leaf) to head (root), while we measure the depth (of an ocean) from earth’s surface (root) to ocean bed (leaf).
Possible Implementation
The main challenge is to “re-balance” the tree when needed. To determine
if a tree needs to be re-balanced, one has to compute its “balance
factor”, obtained by substracting the right subtree height from the left
subtree height. This is done below in the SubtreeBalance method.
Consider the following:
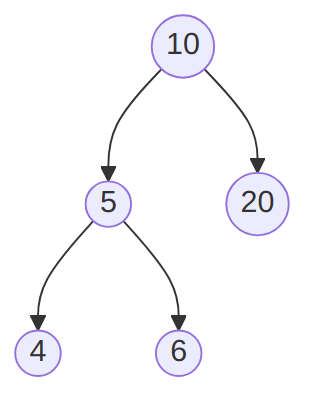
After inserting 2, the tree becomes:
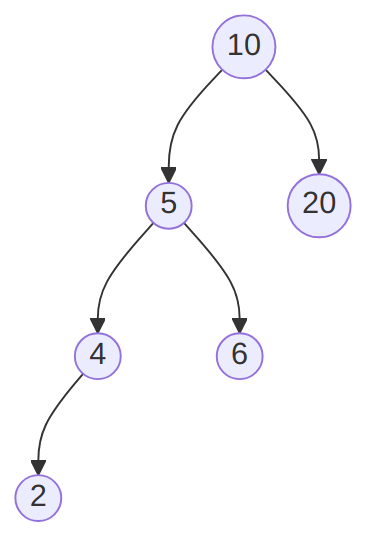
which needs to be re-balanced using the RotateleftChild method given
below. Indeed it is “left-heavy”, on the left-hand side (because the
left sub-tree, with root 5, is deeper, because of its left side).
If, re-using the same example, we insert 7, then the tree becomes:
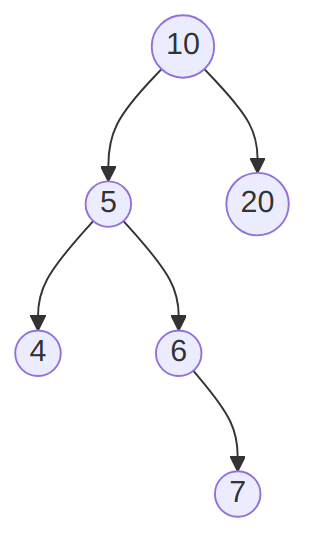
which needs to be re-balanced using the Doubleleftchild method given
below. Indeed it is “left-heavy”, on the right-hand side (because the
left sub-tree, with root 5, is deeper, because of its right side).
Storing the height in the node
using System;
using System.Collections.Generic;
/*
* This implementation of AVL tree is
* "from scratch", and stores the height
* of a node as an attribute instead of
* re-comptuing it when needed.
* This class does not inherit from any
* other class and is "standalone".
*/
public class AVLTree<T>
where T : IComparable<T>
// We need T to realize IComparable
// so that we can decide where to
// insert node, exactly like BSTrees.
{
private class Node
{
public T Data { get; set; }
public Node left;
public Node right;
// Height is implemented as an attribute
// with a property.
private int height;
public int Height
{
get { return height; }
set
{
if (value >= 0)
height = value;
else
throw new ApplicationException(
"The height of a node cannot be less than 0."
);
}
}
public Node(
T dataP = default(T),
Node leftP = null,
Node rightP = null,
int heightP = 0
)
{
Data = dataP;
left = leftP;
right = rightP;
Height = heightP;
}
public override string ToString()
{
return Data.ToString();
}
}
private Node root;
public AVLTree()
{
root = null;
}
public void Clear()
{
root = null;
}
public T FindMin()
{
if (root == null)
throw new ApplicationException(
"FindMin was called on an empty AVL tree."
);
else
return FindMin(root);
}
private T FindMin(Node nodeP)
{
if (nodeP.left == null)
return nodeP.Data;
else
return FindMin(nodeP.left);
}
private int GetHeight(Node nodeP)
{
if (nodeP == null)
return -1;
else
return nodeP.Height;
}
// We have a method to update the height
// of a node, and of its sub-trees.
private int UpdateHeight(Node nodeP)
{
int height = -1;
if (nodeP != null)
{
int nodeLeft = UpdateHeight(nodeP.left);
int nodeRight = UpdateHeight(nodeP.right);
height = Math.Max(nodeLeft, nodeRight) + 1;
nodeP.Height = height;
}
return height;
}
// The following will return
// a negative number if subtree is right-heavy
// a positive number if subtree is left-heavy
// 0 if the subtree is perfectly balanced.
private int SubtreeBalance(Node nodeP)
{
UpdateHeight(nodeP.left);
UpdateHeight(nodeP.right);
// The resulting value is essentially
// nodeP.left.Height - nodeP.right.Height
// but we need to account for null values.
int balance = 0;
if (
!(nodeP == null)
&& !(nodeP.left == null && nodeP.right == null)
)
{
// If nodeP is null, or if nodeP has no children,
// then balanceP is 0. Otherwise, we compute it:
if (nodeP.left == null)
{
balance = -(nodeP.right.Height + 1);
}
else if (nodeP.right == null)
{
balance = nodeP.left.Height + 1;
}
else
{
balance = nodeP.left.Height - nodeP.right.Height;
}
}
return balance;
}
public void Insert(T valueP)
{
root = Insert(valueP, root);
}
/*
* Before
* nodeTop --> A
* / \
* nodeLeft--> B C
* / \
* D E <-- nodeLeft.right
*
* After
* B
* / \
* D A
* / \
* E C
*/
private Node RotateleftChild(Node nodeTop) // Aka left-left rotation
{
Node nodeLeft = nodeTop.left;
nodeTop.left = nodeLeft.right;
nodeLeft.right = nodeTop;
// update heights
nodeTop.Height =
Math.Max(
GetHeight(nodeTop.left),
GetHeight(nodeTop.right)
) + 1;
nodeLeft.Height =
Math.Max(GetHeight(nodeLeft.left), GetHeight(nodeTop))
+ 1;
return nodeLeft; // attached to caller as the new top of this subtree
}
/*
* Before
* nodeTop --> A
* / \
* B C <-- nodeRight
* / \
* D E
*
* After
* C
* / \
* A E
* / \
* B D
*/
private Node RotaterightChild(Node nodeTop) // Aka right-right rotation
{
Node nodeRight = nodeTop.right;
nodeTop.right = nodeRight.left;
nodeRight.left = nodeTop;
// update heights
nodeTop.Height =
Math.Max(
GetHeight(nodeTop.left),
GetHeight(nodeTop.right)
) + 1;
nodeRight.Height =
Math.Max(
GetHeight(nodeRight.left),
GetHeight(nodeTop)
) + 1;
return nodeRight; // attached to caller as the new top of this subtree
}
/*
* Before
* nodeP --> A
* / \
* B C
* / \ / \
* D E F G
*
* After RotaterightChild
* A
* / \
* E C
* / / \
* B F G
* /
* D
*
* After
* E
* / \
* B A
* / \
* D C
* / \
* F G
*
* The simplified version is:
* Before:
* A
* /
* B
* \
* E
* After:
* E
* / \
* B A
*/
private Node DoubleleftChild(Node nodeP)
{
nodeP.left = RotaterightChild(nodeP.left);
return RotateleftChild(nodeP);
}
private Node DoublerightChild(Node nodeP)
{
nodeP.right = RotateleftChild(nodeP.right);
return RotaterightChild(nodeP);
}
// Note that the following method could also use
// SubtreeBalance to compute if the tree needs to be
// re-balanced, instead of using GetHeight directly.
private Node Insert(T valueP, Node nodeP)
{
if (nodeP == null)
return new Node(valueP, null, null, 0);
else if (valueP.CompareTo(nodeP.Data) < 0) // valueP < nodeP.Data --> go left
{
nodeP.left = Insert(valueP, nodeP.left);
if (
(GetHeight(nodeP.left) - GetHeight(nodeP.right))
== 2
)
{
if (valueP.CompareTo(nodeP.left.Data) < 0)
{
nodeP = RotateleftChild(nodeP);
}
else
{
nodeP = DoubleleftChild(nodeP);
}
}
}
else if (valueP.CompareTo(nodeP.Data) > 0) // valueP > nodeP.Data --> go right
{
nodeP.right = Insert(valueP, nodeP.right);
if (
(GetHeight(nodeP.right) - GetHeight(nodeP.left))
== 2
)
{
if (valueP.CompareTo(nodeP.right.Data) > 0)
{
nodeP = RotaterightChild(nodeP);
}
else
{
nodeP = DoublerightChild(nodeP);
}
}
}
else // valueP == nodeP.Data
{
throw new ApplicationException(
"Tree did not insert "
+ valueP
+ " since an item with that value is already in the tree."
);
}
nodeP.Height =
Math.Max(
GetHeight(nodeP.left),
GetHeight(nodeP.right)
) + 1;
return nodeP;
}
public bool Remove(T value)
{
return Remove(value, ref root);
}
private bool Remove(T value, ref Node nodeP)
{
bool found = false;
if (nodeP != null)
{
if (value.CompareTo(nodeP.Data) < 0) // value < nodeP.Data, check left subtree
{
found = Remove(value, ref nodeP.left); // similar to BST's find and remove method
if (SubtreeBalance(nodeP) <= -2) // negative balance means heavy on right side
{
if (SubtreeBalance(nodeP.right) <= 0) // children in straight line
nodeP = RotaterightChild(nodeP); // rotate middle up to balance
else
nodeP = DoublerightChild(nodeP); // children in zig patter - needs double rotate to balance
}
}
else if (value.CompareTo(nodeP.Data) > 0) // value > nodeP.Data, check right subtree
{
found = Remove(value, ref nodeP.right);
if (SubtreeBalance(nodeP) >= 2)
{
if (SubtreeBalance(nodeP.left) >= 0)
nodeP = RotateleftChild(nodeP);
else
nodeP = DoubleleftChild(nodeP);
}
}
else // The value was found!
{
found = true;
if (nodeP.left != null && nodeP.right != null) // Two children
{
nodeP.Data = FindMin(nodeP.right);
Remove(nodeP.Data, ref nodeP.right);
if (SubtreeBalance(nodeP) == 2) // Need to rebalance
{
if (SubtreeBalance(nodeP.left) >= 0)
nodeP = RotateleftChild(nodeP);
else
nodeP = DoubleleftChild(nodeP);
}
}
else
{
nodeP = nodeP.left ?? nodeP.right; // replace with one or no child
// This is equivalent to
// if (nodeP.left == null){
// nodeP = nodeP.right;
// } else { nodeP = nodeP.left;}
// Observe that if both are null, then nodeP simply
// becomes null, as expected.
}
}
}
return found;
}
// The ToString method is simply here to help us debug.
// It is not really pretty, but using pre-order and spaces
// to make it easier to understand how the tree is
// constructed.
public override string ToString()
{
string returned = "";
if (root != null)
{
returned += Stringify(root, 0);
}
return returned;
}
private string Stringify(Node nodeP, int depth)
{
string returned = "";
if (nodeP != null)
{
for (int i = 0; i < depth; i++)
{
returned += " ";
}
returned += nodeP + "\n"; // Calls Node's ToString method.
if (nodeP.left != null)
{
returned += "L" + Stringify(nodeP.left, depth + 1);
}
if (nodeP.right != null)
{
returned += "R" + Stringify(nodeP.right, depth + 1);
}
}
return returned;
}
}Computing the height on the fly
It is also possible to compute the height of nodes “on the fly” instead of storing it.
This archive demonstrates this concept while additionally
- inheriting from the
BTreeclass explored previously, - adding an
IBTreeclass that allows you to explore the re-balancing methods more freely, - containing some examples showcasing how re-balancing works.
Additional Example
Consider the following example:
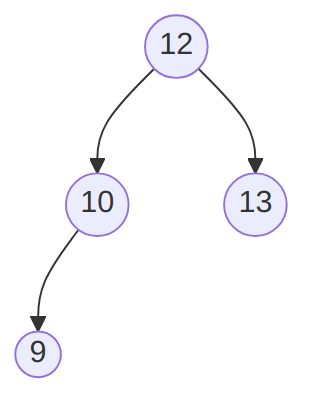
After inserting 8, the tree would become un-balanced and require to call
RotateleftChild:
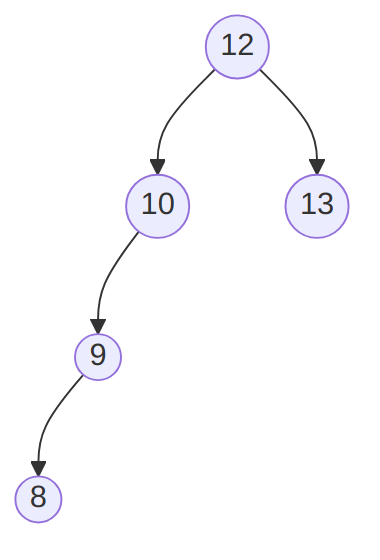
The detail to note here is that RotateleftChild is called with
nodeTopbeing 10,nodeLeftbeing 9,- and
nodeLeft.Rightbeingnull,
aka, going from

to

and since the node with value 8 remains the right child of the node with
value 9, we obtain (marking explicitely the null node that was
manipulated):
