Our goal is to provide our own implementation of Lists, instead of using the one provided by C#‘s System.Collections.Generic namespace. This will help in

understanding how a simple data structure is implemented,
understanding the differences between arrays and lists,
developing simple algorithms traversing lists,
visually representing how lists operate.

The “custom” implementation of list can be found in this project, it is also extended in this project with many additional methods.

Getting Started

Consider the following code:

using System;
 
public class CList<T>
{
  // A CList is … a Cell.
  private Cell first;
 
  // By default, a CList contains only an empty cell.
  public CList()
  {
    first = null;
  }
  // A Cell is itself two things:
  // - An element of data (of type T),
  // - Another cell, containing the next element of data.
  // We implement this using automatic properties:
  private class Cell
  {
    public T Data { get; set; }
    public Cell Next { get; set; }
 
    public Cell(T dataP, Cell nextP)
    {
      Data = dataP;
      Next = nextP;
    }
  }
 
  // A method to add a cell at the beginning
  // of the CList (to the left).
  // We call it AddF for 'Add First'.
  public void AddF(T dataP)
  {
    first = new Cell(dataP, first);
  }
  // The updated CList starts with a cell holding dataP and 
  // a Cell referencing the previous first cell.
}

(Download this code)

The first two important observations are that

Our CList class uses a generic type parameter (the <T> notation), so that we can create CLists containing bool, int, char, etc.,
Our CList class contains itself a class, called Cell.

Cell Class

Let us discuss the Cell class briefly. A Cell has two properties:

Data, of type T, will hold the actual data: if we are creating a CList of ints, then each cell will hold an int in its Data property,
Next, of type Cell, which contains a reference to the next Cell.

A Cell holding the Data of type int 12 and that has for Next value the Cell null will be represented as follows:

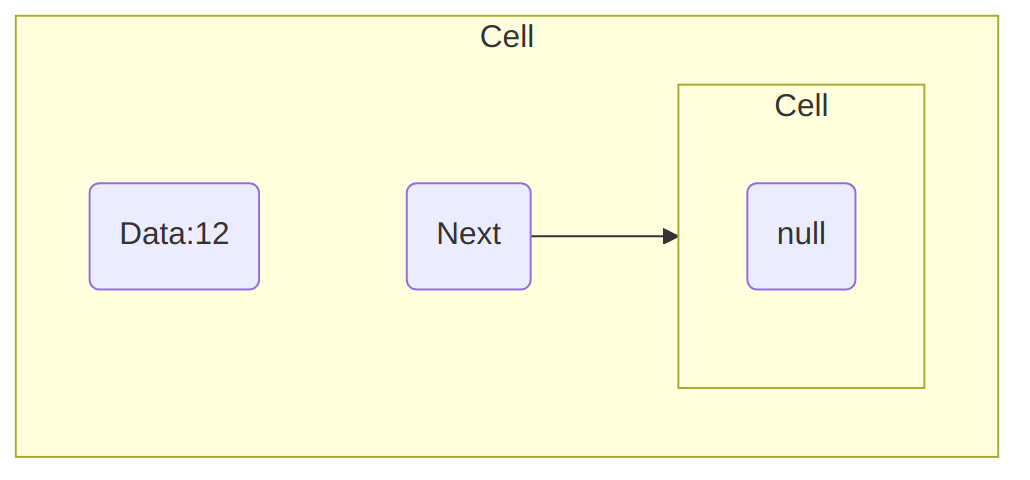
A diagram for a cell holding value 12 (text version, image version, svg version)

Intuitively, a Cell holds a piece of value (Data) and the “address” (more precisely, the reference) to the next Cell: “linking” Cells together is what gives (singly) linked lists, which is the correct technical term for the type of list we are implementing (there are other ways of implementing lists).

CList Class

Creating an object

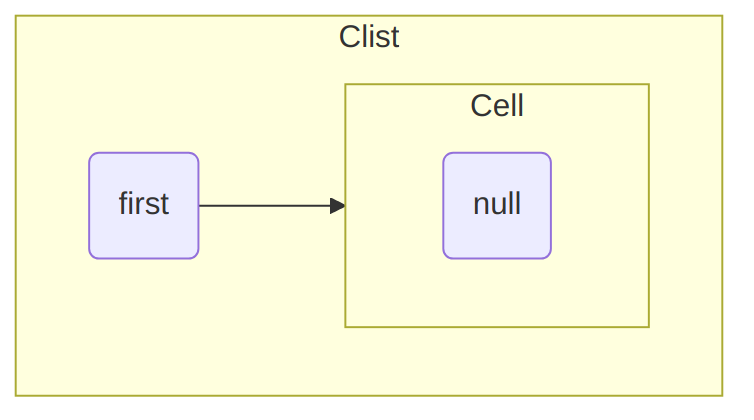
Now, let us zoom back and look at the CList class: a CList object has only one attribute, called first, which is a Cell. When a CList object is created, using for example the following:

    CList<int> myList1 = new CList<int>();

then its first Cell is simply null:

  public CList()
  {
    first = null;
  }

We represent this situation as follows:

A diagram for a CList with only a null cell (text version, image version, svg version)

Adding a Cell to a CList

To start adding elements to our CList myList1, we use the AddF method:

  public void AddF(T dataP)
  {
    first = new Cell(dataP, first);
  }

as follows:

    myList1.AddF(12);

This method does the following:

It creates a Cell hoding dataP as its data, the “previous” first as its Next,
It updates first so that it refers this new Cell.

We would represent this situation as follows:

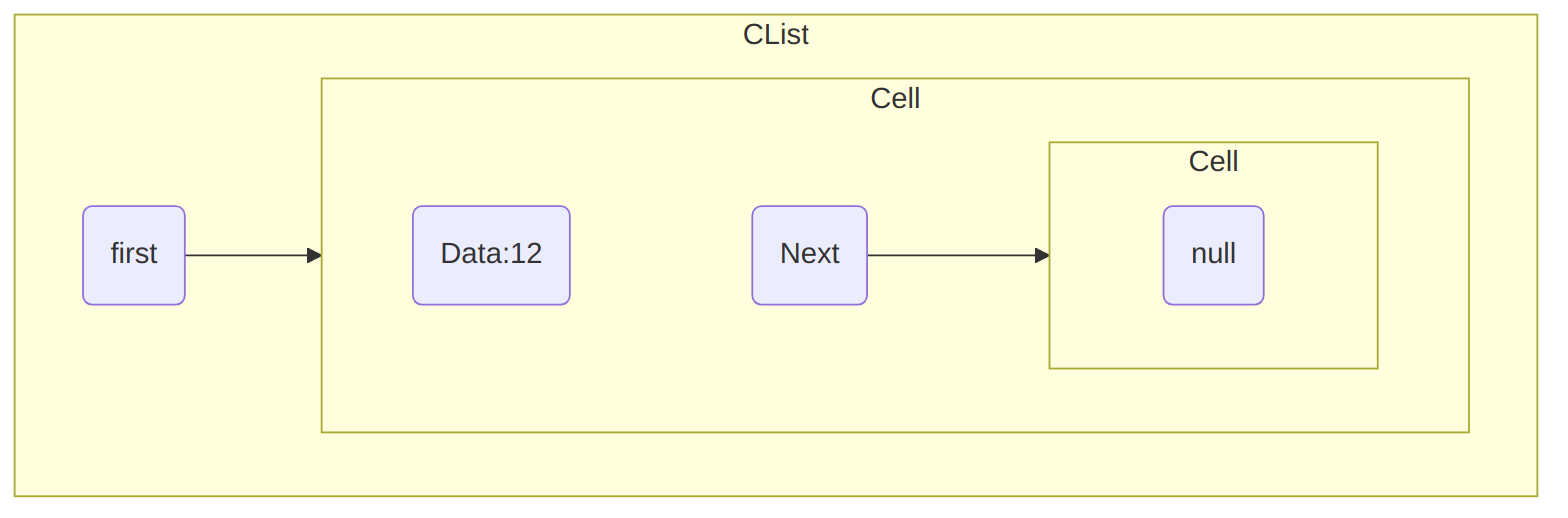
A diagram for a CList with 1 non-null cells, holding 12 (text version, image version, svg version)

Note that

Our CList now contains two Cells objects, the second being null,
first now refers a Cell that actually contains a value, 12.

We can add another element to our list using the following statement:

    myList1.AddF(10);

and our myList1 becomes:

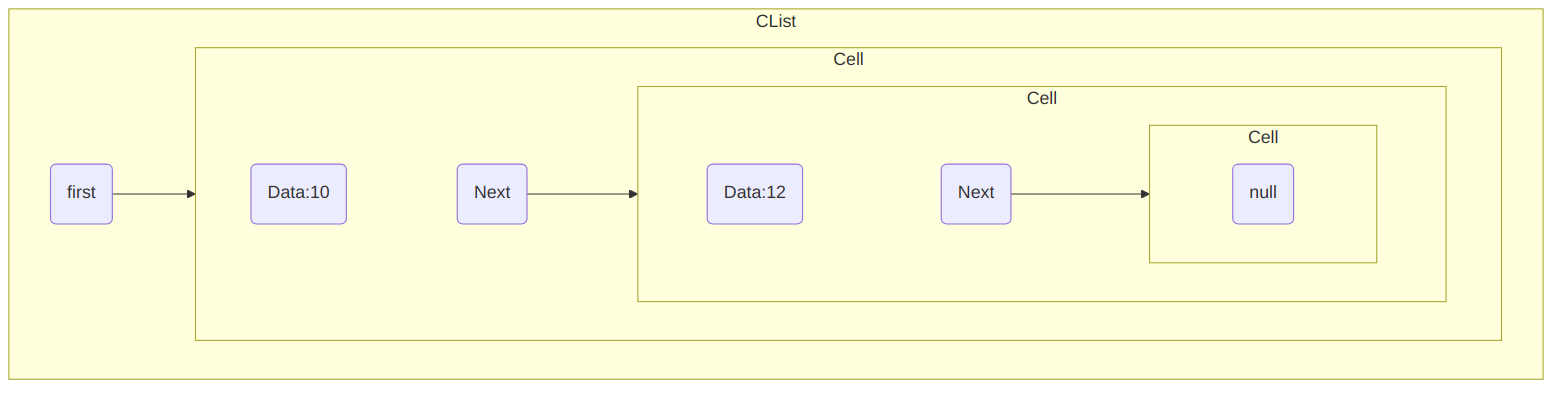
A diagram for a CList with 2 non-null cells, holding 10 and 12 (text version, image version, svg version)

Note that the element is added to the left, that is, the CList “grows” from the left using the AddF method.

More Advanced Methods and Properties

IsEmpty Method and Property

We will often need to test if a CList is empty, so we introduce a method to perform this test easily:

    public bool IsEmpty()
    {
        return (first == null);
    }

Note that we could have decided to implement this test as a property, using for example

public bool IsEmpty
{
    get {return first == null;
}

Of course, such property would not have any set method.

AddL Method

Our AddF method allows to add elements to our CList “to the left”, but we may want to add elements to the end of the list (that is, to its right). We can achieve this with the following method:

    public void AddL(T dataP)
  {
    if (IsEmpty())
      AddF(dataP);
    else
    {
      Cell cCell = first;
      while (cCell.Next != null)
      // As long as the cCell Cell has a neighbour…
      {
        cCell = cCell.Next;
        // We move the cCell cell to this neighbour.
      }
      // When we are done, we can insert the cell.
      cCell.Next = new Cell(dataP, null);
    }
  }

The method proceeds as follows:

If the CList is empty, then we can use AddF, since adding to the right or to the left will have the same outcome,
If it is not, we need to find the “last” Cell. Finding the “last” Cell is easy: it is the only one whose Next is null. We move through the list as follows:
```
Cell cCell = first;
while (cCell.Next != null)
{
    cCell = cCell.Next;
}
```
The idea being that as long as the current Cell contains a Next that is not null, then we follow it and make the next cell our current Cell.
Once we found this “last” Cell, we update its Next so that it refers to a new Cell object that contains the data we wanted to insert (dataP), and does not refers to any other Cell (hence, its Next is null).

Size Property

It can be useful to easily know how many non-null Cells are contained within a CList: this is the equivalent of the Count property from C#‘s List. Of course, this property should only contain a get, since the Size will be computed based on the number of elements contained in the CList, so that we get:

  public int Size
  {
    get
    {
      int size;
      if (IsEmpty())
      {
        size = 0;
      }
      else
      {
        size = 1;
        Cell cCell = first;
        while (cCell.Next != null)
        // As long as the cCell Cell has a neighbour…
        {
          cCell = cCell.Next;
          // We move the cCell cell to this neighbour.
          size++;
        }
      }
      return size;
    }
  }

This property uses a loop very similar to the AddL method to traverse the CList, but it keeps track of how many elements were traversed using a size index. Note that it begins by testing if the CList is empty: otherwise, the condition cCell.Next != null would throw an exception with an empty CLists, since null does not posses a Next property!

ToString Method

We also implement a ToString method that returns a table looking like an array:

 
  public override string ToString()
  {
    string returned = "———";
        // Line above the table
    for (int i = 0; i < Size; i++)
    {
      returned += "————";
    }
    returned += "\n| ";
        // Content of the CList
    Cell cCell = first;
    while (cCell != null)
    {
      returned += $"{cCell.Data} | ";
      cCell = cCell.Next;
    }
    returned += "\n———";
        // Line below the table
    for (int i = 0; i < Size; i++)
    {
      returned += "————";
    }
    return returned + "";
  }

Our previous myList1 would then be displayed as follows:

———————————
| 10 | 12 |
———————————

Observe that:

We use the Size property to draw the lines above and below our table, repeating the same code twice.
The string "———" is added once to the line above and once to the line below the table to improve the final rendering.
Our loop uses the cCell != null condition, testing if a Cell is null before trying to access its Data property. Note that cCell will hold null at some point, but no exception will be raised since our condition makes the loop terminates when that happens.
Attempting to call ToString with a CList containing only the null Cell would return
```
———
|
———
```
which is not very elegant, but at least no exception is raised.

Additional Methods and Properties

Additional methods are shared in the following source code:

  public T Access(int index)
  {
    if (index >= Size)
    {
      throw new IndexOutOfRangeException();
    }
    else // Some IDE will flag this "else" as redundant.
    {
      int counter = 0;
      Cell cCell = first;
      while (counter < index)
      {
        cCell = cCell.Next;
        counter++;
      }
      return cCell.Data;
    }
  }
 
  /*
   * We can write four methods to
   * remove elements from a CList.
   * - One that clears it entirely,
   * - One that removes the first cell,
   * - One that removes the last cell,
   * - One that removes the nth cell, if it exists,
   */
 
  public void Clear()
  {
    first = null;
  }
 
  public void RemoveF()
  {
    if (!IsEmpty())
      first = first.Next;
  }
 
  public void RemoveL()
  {
    if (!IsEmpty())
    {
      if (first.Next == null)
      {
        RemoveF();
      }
      else
      {
        Cell cCell = first;
        while (
          cCell.Next != null && cCell.Next.Next != null
        )
        {
          cCell = cCell.Next;
        }
        cCell.Next = null;
      }
    }
  }
 
  // Method to remove the nth element if it exists.
  public void RemoveI(int index)
  {
    if (index > Size)
    {
      throw new IndexOutOfRangeException();
    }
    else // Some IDE will flag this "else" as redundant.
    {
      int counter = 0;
      Cell cCell = first;
      while (counter < index - 1)
      {
        cCell = cCell.Next;
        counter++;
      }
      cCell.Next = cCell.Next.Next;
    }
  }
 
  // Method to obtain the largest
  // number of consecutive values
  // dataP.
 
  public int CountSuccessive(T dataP)
  {
    int cCount = 0;
    int mCount = 0;
    Cell cCell = first;
    while (cCell != null)
    {
      if (cCell.Data.Equals(dataP))
      {
        cCount++;
      }
      else
      {
        if (cCount > mCount)
        {
          mCount = cCount;
        }
        cCount = 0;
      }
      cCell = cCell.Next;
    }
    if (cCount > mCount)
    {
      mCount = cCount;
    }
    return mCount;
  }
 
  // Method to remove at a particular index
  // Very similar to RemoveI, simply
  // implemented with a different philosophy.
  public void RemoveAt(int index)
  {
    if (index >= 0 && index < Size)
    {
      if (index == 0)
        RemoveF();
      else if (index == (Size - 1))
        RemoveL();
      else
      {
        Cell cCell = first;
        for (int i = 0; i < index - 1; i++)
        {
          cCell = cCell.Next;
        }
        cCell.Next = cCell.Next.Next;
      }
    }
    else
      throw new ArgumentOutOfRangeException();
  }
 
  // Method to reverse a list
  public void Reverse()
  {
    Cell cCell = first;
    Cell previous = null;
    Cell next;
    while (cCell != null)
    {
      next = cCell.Next;
      cCell.Next = previous;
      previous = cCell;
      cCell = next;
    }
    first = previous;
  }
 
  // Method to look for a specific value (recursively)
  public bool Find(T dataP)
  {
    return Find(first, dataP);
  }
 
  private bool Find(Cell cCell, T dataP)
  {
    if (cCell == null)
      return false;
    else if (cCell.Data.Equals(dataP))
      return true;
    else
      return Find(cCell.Next, dataP);
  }
 
  // Method to obtain the last index
  // of dataP.
  public int LastIndexOf(T dataP)
  {
    int index = 0,
      lastIndex = -1;
    Cell cCell = first;
    while (cCell != null)
    {
      if (cCell.Data.Equals(dataP))
      {
        lastIndex = index;
      }
      index++;
      cCell = cCell.Next;
    }
    return lastIndex;
  }
 
  // Recursive method to obtain the
  // frequency of dataP
  public double Frequency(T dataP)
  {
    if (Size == 0)
      throw new ArgumentNullException();
    else
      return Count(dataP, first) / (double)Size;
  }
 
  private int Count(T dataP, Cell pTmp)
  {
    if (pTmp == null)
      return 0;
    else if (pTmp.Data.Equals(dataP))
      return 1 + Count(dataP, pTmp.Next);
    else
      return 0 + Count(dataP, pTmp.Next);
  }

(Download this code)

ℙrinℂomℙ

Explorer

Custom Implementation of Lists